Mallard-Basic gegen Visual-Basic


Das Programm mit dem phantasievollen Namen Polyominoes für den PCW wurde vor 5 - 6 Jahren von Ed Oakeley für einen Freund geschrieben; auf einem - wie er sagt !!! - alten Amstrad PCW. Nun war ich (= wnb) Mitte August letzten Jahres (!!!) im Internet auf der Suche nach 'Futter für den JOYCE' und stieß dabei auf Ed's Homepage, auf der er dieses skurrile JOYCE-Programm vorstellte. Via elektronischer Post (= eMail) nahm ich Kontakt zu Ed auf und mittlerweile ist Ed Mitglied unserer Arbeitsgemeinschaft; er hat uns auch gleich sein Progy für den Klub zur Verfügung stellte. Ein kleinen Haken hat die ganze Sache natürlich: Ed ist Engländer und bediente sich seiner Muttersprache, als er nachfolgende Anleitung zu seinem Progy verfaßte. Alois Festini war so freundlich, den Text für uns zu übersetzen und das Progy zu testen:


Die Grundidee ist ganz einfach: Wie viele verschieden Formen kann man von einer vorgegebenen Anzahl von Quadraten (Vierecken) machen, wobei es nur erlaubt sein sollte, daß sie sich nur an den Kanten berühren (z.B. kann eine Ecke kein Ort des alleinigen Kontakts sein). Jedes Spiegelbild oder jede Drehung darf nicht gezählt werden, da sie dieselbe Form haben, nur irgendwie im Raum bewegt.

Nach 1, 2 und 3 Quadraten steigt die Anzahl an Mustern dramatisch an, einige können recht nett aussehen.


Der Amstrad PCW ist ein kurioses Tier, da Mallard Basic (der kostenlose Basic-Interpreter ist damit ausgerüstet) einige sehr starke Routinen besitzt, um indizierte Datenbanken zu schreiben. Der Autor (= Ed Oakeley) mußte erkennen, daß die Anzahl von Kombinationen ganz schön zunahm, und jenseits von 11 Quadraten bekam er erste Probleme: 1. Mit der Geschwindigkeit (JOYCE ist nun 'mal nicht der schnellste) und 2. Mit dem Speicherplatz auf der Diskette - beschränkt auf rund 700 kB, sofern man keine Festplatte hat.

Die anfängliche (ziemlich dürftige) Lösung war, einen CP/M-Emulator für einen 486dx4-100 PC zu bekommen und das Amstrad-Programm hierunter laufen zu lassen. Dies funktionierte, aber es war immer noch schrecklich langsam, denn der Emulator schien hartnäckig nicht nur die Befehle abzuarbeiten, sondern auch die Geschwindigkeit des Z80-Programms. Inzwischen hat der Autor das Programm nach 'Visual Basic' übertragen, und es läuft etwas schneller, aber es sind ein paar unerwartete Fehler aufgetreten; veranlaßt dadurch, daß das Micosoft-Access-Datenbank-Format weniger flexibel (!) ist als die Jetsam-Datenverwal-tung unter Mallard Basic. ÄSchmunzelsanmerkung wnb: JOYCE schlägt wieder einmal den PC !Ü Das Hauptproblem ist, daß es Schwierigkeiten zu haben scheint, mit Indexen umzugehen, die aus 8-Bit-zeichen gebildet werden. (Der Autor arbeitet mit allen 256 ASCII-Zeichen, um jede Form zu verschlüsseln und in der Datenbank unterzubringen. Er arbeitet weiterhin an seinem Programm und möchte eine Windows Betaversion erstellen).


Der Grund für das Erarbeiten dieses Programms liegt darin, daß Ed einem Freund, der nächtelang vor dem Zeichenpapier saß, zeigen wollte, daß ein Computer die Muster schneller und genauer erstellen kann (es funktioniert - beim normalen PCW 8512 allerdings nur bis zu 11 Quadraten).


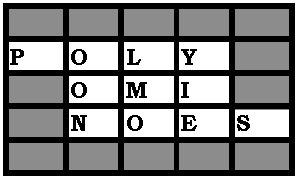
Programm-Test: Alois Tests haben ergeben, daß die Kombinationsmöglichkeiten so enorm ansteigen, daß lange Zeit vor dem Computer zugebracht werden muß, um alle Varianten darstellen zu lassen. Alois ermittelte folgende Werte:


Anzahl der QuadrateKombinationsmöglichkeiten
2
3
4
6
7		1
2
5
36
108		 


Ferner stellte Alois fest, daß Ed's Polyominoes zwar die Kombinationsmöglichkeiten korrekt auf dem Bildschirm darstellt, aber die Anzahl eben dieser Kombinationen falsch berechnet. Wen's interessiert (ich hoffe doch wohl jeden), kann das Progy selbst ausprobieren; es befindet sich auf unserer Diskette zur Klubzeitung KaD53. Die Festplattenbesitzer könnten ja 'mal austesten, wie viele Kombinationsmöglichkeiten es bei ... sagen wir ... 20 Quadraten gibt ?! Vielleicht lesen wir ja in einer der nächsten Klubzeitungen wieder etwas über 'Polyominoes und die Unmöglichkeiten der Vielfalt.'


Programmautor: Ed Oakely
Gesurft: wnb - 21.08.1997
Übersetzt: Alois Festini - 03.10.1997






Zur Person ... Edward James Oakeley,  Jahrgang 1970, ist - wie könnte es für einen JOYCE-User der Ersten Stunde anders sein - Brite ! Er studierte an der Universität in Bristol Biochemie (!) und arbeitet seit 1995 in der Schweiz am 'Friedrich Miescher-Institut' in Basel an der Analyse der 'DNA höherer Pflanzen und Tiere'. Er hat zu diesem Fachgebiet auch schon mehrere Publikationen veröffentlicht und beschäftigt sich auf seiner Internet-Homepage u.a . mit dem Polyominoes-Phänomen, das er - siehe oben - bereits vor Jahren mit dem JOYCE bearbeitete.



Polyominoes - eine Wissenschaft für sich ?!


Ein Jahr hat es gedauert, bis ich Zeit, Muße und vor allen Antworten zu Polyominoes fand. Schöne Sache ... hat irgendetwas mit Mathematik, Spiel und Geometrie zu tun ... schauen wir doch 'mal im Lexikon unter POLYOMINOES nach: Fehlanzeige ... Fehlanzeige ... Fehlanzeige ... Fehlanzeige


Wie soll man über etwas berichten, das einem selber noch nicht ganz klar ist ? Gut, es geht darum, eine bestimmte Anzahl von Quadraten in Manier einer Patience aneinander zu legen und die verschiedenen Kombinationsmöglichkeiten herauszufinden ... macht sogar Spaß ... aber eine Lebensaufgabe könnte dies für mich nicht werden [smile]. Aber kann man diese Polyominoes auch zwischen-durch-spielen, z.B. wenn man in irgend einem Wartezimmer sitzt ... man benötigt nur einen Kugelschreiber [zur Not gibt's den am Tresen bei der Anmeldung] und ein Stück Papier [z.B. die im Wartezimmer ausliegenden Zeitschriften] ...smile ... es möge jeder 'mal ausprobieren: z.B. mit vier Quadraten kann man fünf Kombinationen zusammenlegen [siehe Skizzen im vorangehenden Bericht] und mit fünf Quadraten, da gibt es ... aber das probiert 'mal selber aus :).


Nun, an irgendetwas erinnert mich die ganz Sache doch ... gibt es da nicht ein japanisches [oder war's chinesisches] Legespiel mit Dreiecke(n), die so angeordnet werden müssen, das Tierfiguren etc. entstehen. Etwas für sehr Geduldige. Ahh ... Geduldsspiele ! Was gab es da noch alles ?! Solitär, Rubik's Zauberwürfel, Schiebepuzzle, Puzzle allgemein und im besonderen: 3D-Puzzle oder sogen. Lunatic-Puzzle - Ineinandergesteckte Holzklötze, die man, nach dem man so übermütig war, sie auseinanderzunehmen, nur mit viel logischem Denken wieder zusammen basteln kann. Oder wer kennt den Holzring nicht, der unzertrennlich ?!? durch eine Schnur mit einer Holzkugel verbunden scheint ?! Oder die auf ewig ?!? ineinander verkeilten Büroklammern ?!


Polyominoes zählt also zur Kategorie der Gedulds- & Geschicklichkeits-Spiele ! Bestätigung fand ich nach langer Suche im Solomon W. Golombs Buch "Polyominoes, Puzzles, Patterns, Problems and Packings" [Sorry: englischsprachig ... und sorry: http://www.johnrausch.com/PuzzleWorld/].


VERBINDUNGEN ... Alle, die sich gerne in Geduld üben, Legepuzzle oder Patiencen lieben, seien an dieser Stelle auf das JOYCE-Spiel VERBINDUNGEN hingewiesen ... Databox zur ehemaligen Zeitschrift cPCw-Amstrad-Intenational Nr. 2 / 1990.




Abgedruckt in Klubzeitung Nr. 53. Autor: wnb // 31. August 1998